Linear Demand, Elasticity, and Total Revenue
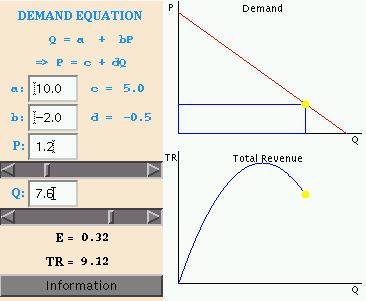
To find out how to work the applet controls, see the instructions
below.
This applet is designed to help you visualize the relationship between
a linear demand curve, elasticity, and the total revenue
of
a monopolist. The total revenue may also be thought of as
the total expenditure by consumers.
Contents
Linear Demand
The Demand Equation
The first demand equation beginning economics students usually see is
that of a linear, or straight-line demand curve. This is the simplest
type of equation to work with. Economists write the equation for
demand in the following form:
| Q = a + bP |
(demand equation)
|
Q is on the left-hand side because we usually think of the quantity
demanded as depending on price and not the other way around. So Q
is the dependent variable. That is, we consider Q to
be a function of P, so the demand equation may also be written as
| Q(P)= a + bP |
(Q written as a function of P)
|
which emphasizes the dependence of Q on P.
The parameters a and b are called the intercept and slope,
respectively. The value of a tells us what the value of Q
will be when P is equal to zero. The value of b,
tells us the amount of change in Q that will occur due to a unit
change in P. The value of b will always be negative,
meaning that P and Q move in opposite directions,
because the law of demand tells us that when the price goes up,
the quantity demanded goes down.
The Inverse Demand Equation
According to tradition, when economists draw a demand curve in a two
dimensional diagram, they put the price on the vertical axis, and the quantity
on the horizontal axis, like the diagram in the upper right corner of the
applet. Mathematical tradition dictates that the dependent variable
be drawn on the vertical axis, and the independent variable be drawn on
the horizontal. Thus, we must also be able to think of P as
function that is dependent on Q. The function
P(Q),
which is also linear, is called the inverse of the function Q(P).
The corresponding inverse demand equation is written like this:
| P = c + dQ |
(inverse demand equation)
|
If you start with the demand equation Q(P), and do a little algebra
to isolate P on the left-hand side, you can verify that c =
-a/b and d = 1/b. Since, as we determined above,
the sign of a is positive and the sign of b is negative,
we know from these equalities that c must be positive and d must
be negative.
Go back to the applet.
Elasticity
Elasticity is a measure of the responsiveness of one variable to
changes in some other variable. We are interested in the price
elasticity of demand, which measures the response of the quantity
demanded to a change in price. Formally, the price elasticity of
demand, which we will call E, is the ratio of the percent
change in quantity over the percent change in price.
For small
changes in P and Q, a reasonable approximation of the
percent change in P is the difference between the initial price
P1 and an adjacent price P2
divided by the initial price. The percent change in price is
thus approximately (P2 -
P1)/P1. The approximation of the
percent change in Q is obtained in the same way, where
Q1 = Q(P1) and
Q2=Q(P2). Using these definitions
for percent change, an approximation for elasticity is
 |
(price elasticity approximation)
|
where the vertical bars surrounding the ratio on the
right side of the equation indicates absolute value. The smaller
the change in P, the closer the approximation. It is
possible to calculate an exact value of the elasticity for a small
change in P, call it  P,
using the demand equation Q(P) = a + bP and a little
algebra. Let P1 = P and P2= P
+
P,
using the demand equation Q(P) = a + bP and a little
algebra. Let P1 = P and P2= P
+  P so that
P so that  P = P2 -
P1. Then let
P = P2 -
P1. Then let  Q = Q(P2) -
Q(P1). Substituting the demand equation into the
right side of this equation we get
Q = Q(P2) -
Q(P1). Substituting the demand equation into the
right side of this equation we get
 Q = a + bP2 - (a
+ bP1) = b(P2 - P1) = b
Q = a + bP2 - (a
+ bP1) = b(P2 - P1) = b P.
P.
When we substitute  P
and
P
and  Q
into the exact version of the definition of elasticity, we get the
following:
Q
into the exact version of the definition of elasticity, we get the
following:
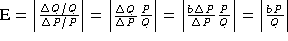 |
(exact price elasticity)
|
Go back to the applet.
|
HOW TO WORK THE APPLET CONTROLS
The equation for demand, Q = a + bP,
and the inverse demand equation, P = c + dQ, are displayed
in the upper left of the applet.
1. The parameters a and b can be changed to any values
that define a downward-sloping curve. Therefore, a must be
a positive number and b must be negative. The parameters of
the inverse demand equation, c and d, will change automatically
when you change a or b. You will probably notice that
entering different values for a and b do not change the appearance
of the demand curve. This is because the applet adjusts the scale
of each axis based on where the demand curve crosses it.
2. P and Q can be changed directly or by dragging
either of the sliders. When you change the value of P or Q,
the corresponding value of the other is changed to maintain the equality
of the equations.
NOTE: When changing any of the 4 values
directly, you must press your Enter or Return
key immediately after editing, while the cursor is still in the box, otherwise
your changes will not take effect.
Go back to the applet. |
Copyright 1997,1998, Geoffrey
Gerdes
Last Update: November 24, 1998
free adult flash games, teen models amateur cuties, black girls anal, asian girl galleries, white ass black dick, dennis leary asshole video, bbw mpg, movies , beach nude sex, beastiality trailers, bikinis off, mmf bisexual threesomes, fat bitch, busty blonde, young teen blowjob video, spanking photos, boob flashing women, ladies leather boots, travesti brazil, brunette sluts, mature butts, amateurs web cam teens, big cartoon boobs, , free celebrety porn, pro cheerleaders topless, hot free naked chicks, gay chubby teens, closeup upskirt, suck my cock, blonde coed babes, dp creampie, cum cunt, american dad porn comics, best online dating sites, baby dick, , free dirty cum sluts, domination & spanking relationships, adult dvd rentals online, hot ebony cumshots, erotica feminine beauty, ethnic strippers, cum on her face orgy, wife facials, gay fantasy sex cartoons, fat cocks, girls toes feet, dangers of female genital mutilation, male pissing fetish, creampie ffm, lesbain fisting, flexible contortionist stretch pussy movies free, free hard core porn, fuck sister, bang gang squad, my wife's gangbang, hardcore gay anal fucking, gothic girls blood, gay boys and dads, group shower fucking, mothers hairy pussy, footjob clips, simpsons hardcore, dbz anime porn, lonely housewives naked, incest mom, free nude indian gallery, nude latin male galleries, hands between her legs, wild lesbians, free lingerie tgp, live virus removal, sybian machine, male maid bondage, male stars nude, dildo masturbation, free mature and girl, big juicy melons, men jerking off boys, bridget the midget nude, milf personals, gay military guys, naked amature moms, teen mouth, milfhunter movies, painted fake nails, nick lachey naked, nipple stretcher, kirsten dunst nude, horny nurse gallery, fucked in nylons, office gang bang, teen oral sex advice, female orgasm video squirting pussy video, high tech outdoor clothing, paris hilton getting fucked, free party hardcore, peep sight for bow, double triple penetration, free porn clips grannies, names of latina pornstars, pregnant women, gay public nudity, lesbian sex lesbian pussy, mouth rape, reality fucking, sex teen redhead, scat free, raunchy schoolgirl, secretary fuck movies free, anal sex, naked shaved women, shemale hentai, shower orgy, biggest silicone tits in the world, young skinny ass, biker sluts, michelle raven smoking during sex, father daughter spanking, stocking fetish gallery, 14k white gold heavy cz stud earrings, suck my, husband swallows cum, honda swaps, tanned naked girls, tattoo skull art, teen breasts, teens wearing thong g strings, dick deep throat, tiny eve, polish tits, xxx toon, sex toy party etiquete, sissy tranny, trans erotica, twink young, uniform tgp, fergie upskirts, diagram of a vagina, video game porn, voyeur toilet bbs, wife webcams, xxx woman, young naked girls, gay youth nad younger, ky zoo, adult toys, free amateur upskirt, anal licking, hot asian men, sexy ass bitches, wide asshole, italian bbw, bdsm strap on, sex at the beach, kristys mpegs beastiality, bikini fitness model, bisexual adult videos, horny bitch, blondes sucking dick, free blowjob samples, schoolgirl bondage, boob cruise mpeg, free boots porn, hotsex brazil, brunette pussy sucking, big butt brazil, web cam masturbation, pokemon cartoon sex, hot celebs nude, celebrety slips, nude teen cheerleaders, big dicks in small chicks, free naked chubby girls, blow job closeup, girl sucking cock, playboy coed of the week, free gaping anal creampie, cum swallowing, , , thick dick penetration, girls first dildo, hot dirty sex, bbw female domination, backup harddrive to dvd, free latina ebony porn, sapphic erotica shower, gay ethnic guys, cute cum face, latina facial, fantasy football free cheat sheets, fat nude women, slutty feet, female cum squirter, angora sweater fetish, , gay triple fisting, flexible porn stars, free hardcore sex, schoolgirl fuck, gang licked, indian gangbang pics, free gay porn big arab black dicks, gothic satanism boylove, dad daughter fuck, group bang, hairy mexican pussy, , hardcore granny fucking, uncensored hentai, , mom and son incest cum, free indian sex videos, big beautiful sexy latin men, hairy legs boxers, ebony lesbian, teen lingerie gallery pics, live spy cams, hentai machine, hentai lesbian maid, male cumshots, hardcore hentai masturbation, older women free pics, huge round black melons, asian gay men, midget cum pussy, milfs sucking dick, military sampling for quality, busty mom thumbs, poop mouth, black anal movies, creative nails foundation course, naked preteens, accidental nipple slip, nude male celebs, handjob nurse, open toed shoes with nylons sex, lesbian office sex free, deep penetration oral sex, orgasms during gnancy, outdoor advertising billboards leasing, paris hilton crotch shot, cfnm party cum, adult little bo peep costumes, hentai double penetration, soft core porn, famous indian pornstars, pregnant model, public restroom sex, black ass and pussy, interracial rape, sex reality, , scat porn videos, schoolgirl kissing, legal secretary career, pam anderson sex, hot virgin pussy shaved, shemale comix, teen shower sex, huge silicone tits nude, mormon girl skinny dipping, dildo sluts, boys smoking, good old fashioned spanking clip, stockings shemale, sexy teen studs, suck my cock, free teen cum swallow, total return swap, tanned thong girls, gang tattoos identify symbols, asian teen, lace thong girl, amateur throat, tiny nude chicks, great tits and ass, free toon sex videos, homemade vagina toys sex, trannys fucking guys, trans gogo, free boy twink linksl, martial arts uniform, upskirt with no panties, vagina stretching, milf seeker videos, voyeur nude, wife slut, xxx vogue sex, hot young teen lesbians, child youth hockey jersey, florida zoo,


![]() P,
using the demand equation Q(P) = a + bP and a little
algebra. Let P1 = P and P2= P
+
P,
using the demand equation Q(P) = a + bP and a little
algebra. Let P1 = P and P2= P
+ ![]() P so that
P so that ![]() P = P2 -
P1. Then let
P = P2 -
P1. Then let ![]() Q = Q(P2) -
Q(P1). Substituting the demand equation into the
right side of this equation we get
Q = Q(P2) -
Q(P1). Substituting the demand equation into the
right side of this equation we get
![]() Q = a + bP2 - (a
+ bP1) = b(P2 - P1) = b
Q = a + bP2 - (a
+ bP1) = b(P2 - P1) = b![]() P.
P.![]() P
and
P
and ![]() Q
into the exact version of the definition of elasticity, we get the
following:
Q
into the exact version of the definition of elasticity, we get the
following: